random【擬似乱数】3.2 / 3.6 / 3.9 / 3.103.11

メモ  (  概要 状態関数 例 ランダム値生成関数 例 シーケンス操作関数 例 実数値分布関数 例 クラス・関数  )  例

メモ

例

状態関数

import random

# seed(a=None, version=2)【初期化】
for i in range(5):
    print(random.randint(0, 10))
# 出力例：
# 7
# 3
# 4
# 4
# 9

random.seed(1234567)
rnd_1 = [random.randint(0, 10) for i in range(5)]
random.seed(1234567)
rnd_2 = [random.randint(0, 10) for i in range(5)]
for i in range(5):
    print(rnd_1[i], rnd_2[i], (rnd_1[i] == rnd_2[i]))
# 出力例：
# 6 6 True
# 3 3 True
# 1 1 True
# 9 9 True
# 5 5 True

# getstate()【内部状態取得】
random.seed()
for i in range(5):
    print(random.randint(0, 10))
# 出力例：
# 6
# 2
# 10
# 5
# 7

state = random.getstate()
rnd_3 = [random.randint(0, 10) for i in range(5)]

# setstate(state)【内部状態設定】
for i in range(5):
    print(random.randint(0, 10))
# 出力例：
# 1
# 5
# 4
# 9
# 10

random.setstate(state)
rnd_4 = [random.randint(0, 10) for i in range(5)]
for i in range(5):
    print(rnd_3[i], rnd_4[i], (rnd_3[i] == rnd_4[i]))
# 出力例：
# 7 7 True
# 6 6 True
# 0 0 True
# 1 1 True
# 4 4 True

ランダム値生成関数

import random

# getrandbits(k)【ランダム整数生成 (ビット指定)】
for i in range(5):
    k = (i + 1) * 8
    rnd = random.getrandbits(k)
    print(f'({k}) {rnd:#012x} {rnd:#051_b}')
# 出力例：
# (8) 0x0000000075 0b0000_0000_0000_0000_0000_0000_0000_0000_0111_0101
# (16) 0x000000ee40 0b0000_0000_0000_0000_0000_0000_1110_1110_0100_0000
# (24) 0x00002a3226 0b0000_0000_0000_0000_0010_1010_0011_0010_0010_0110
# (32) 0x00945bbef7 0b0000_0000_1001_0100_0101_1011_1011_1110_1111_0111
# (40) 0x159744dc3c 0b0001_0101_1001_0111_0100_0100_1101_1100_0011_1100

# randbytes(n)【ランダムバイト生成】
for i in range(5):
    bytes = random.randbytes(10)
    print(bytes)
# 出力例：
# b'?\xba&x\xbf\x9a\\\x8fSG'
# b'\xeaj\xec\x112D\xfdX2G'
# b'7V\xbf\xe6Ev\xcf\x9e\x19\x00'
# b'{\x87\x87\xb5!2{M\xf3\xe9'
# b'\x96\x98i\x8eL \xc3\xfc\xa5\x90'

# randint(a, b)【ランダム整数生成】
for i in range(5):
    rnd = random.randint(10, 20)
    print(rnd)
# 出力例：
# 11
# 10
# 12
# 20
# 16

# randrange(start, stop[, step])【ランダム整数生成 (等差数列)】
for i in range(5):
    rnd = random.randrange(3, 33, 3)
    print(rnd)
# 出力例：
# 12
# 9
# 6
# 30
# 3

# randrange(stop)【ランダム整数生成 (等差数列)】
for i in range(5):
    rnd = random.randrange(10)
    print(rnd)
# 出力例：
# 8
# 3
# 2
# 1
# 7

# random()【一様分布】
for i in range(5):
    rnd = random.random()
    print(rnd)
# 出力例：
# 0.409240761463217
# 0.1869568160790639
# 0.5550096213832235
# 0.4911721941668322
# 0.24567783064047377

# uniform(a, b)【一様分布 (範囲指定)】
for i in range(5):
    rnd = random.uniform(10, 20)
    print(rnd)
# 出力例：
# 13.947031207983711
# 16.04608572314917
# 10.279244047672474
# 14.887712010294461
# 17.98819298549841

シーケンス操作関数

import random

# choice(seq)【要素選択】
for i in range(3):
    num = random.choice([3, 5, 7, 11, 13, 17])
    print(num)
# 出力例：
# 17
# 3
# 7

for i in range(3):
    char = random.choice('abcxyz')
    print(char)
# 出力例：
# b
# a
# y

population = ['aaa', 'bbb', 'ccc', 'AAA', 'BBB', 'CCC']
for i in range(3):
    word = random.choice(population)
    print(word)
# 出力例：
# CCC
# aaa
# ccc

# choices(population, weights=None, *, cum_weights=None, k=1)【複数要素選択(重複あり)】
population = ['aaa', 'bbb', 'ccc', 'AAA', 'BBB', 'CCC']
seq = random.choices(population, [10, 10, 10, 1, 1, 1], k=6)
print(seq)
# 出力例：['bbb', 'ccc', 'aaa', 'aaa', 'aaa', 'BBB']
seq = random.choices(population, [1, 1, 1, 10, 10, 10 ], k=6)
print(seq)
# 出力例：['BBB', 'AAA', 'CCC', 'BBB', 'CCC', 'AAA']
seq = random.choices(population, cum_weights=[1, 2, 3, 13, 23, 33], k=6)
print(seq)
# 出力例：['BBB', 'BBB', 'CCC', 'CCC', 'AAA', 'AAA']

# shuffle(x[, random])【シャッフル (インプレース)】
x = ['aaa', 'bbb', 'ccc', 'AAA', 'BBB', 'CCC']
random.shuffle(x)
print(x)
# 出力例：['aaa', 'ccc', 'bbb', 'AAA', 'BBB', 'CCC']

# sample(population, k, *, counts=None)【複数要素選択(重複なし)】
population = ['aaa', 'bbb', 'ccc', 'AAA', 'BBB', 'CCC']
seq = random.sample(population, 6)
print(seq)
# 出力例：['CCC', 'BBB', 'aaa', 'bbb', 'AAA', 'ccc']
seq = random.sample(population, 9, counts=[1, 1, 1, 2, 2, 2])
print(seq)
# 出力例：['ccc', 'aaa', 'CCC', 'BBB', 'bbb', 'BBB', 'CCC', 'AAA', 'AAA']

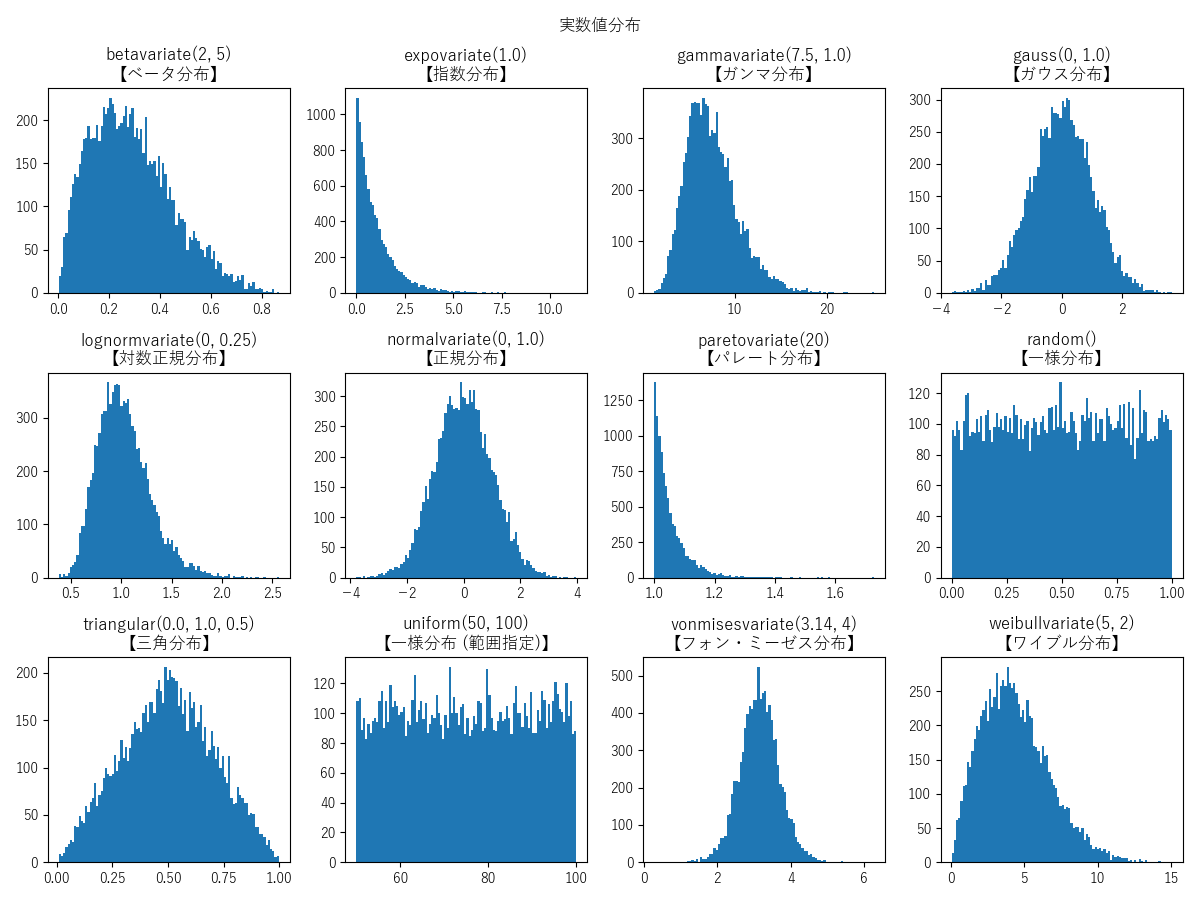
実数値分布関数

外部ライブラリの matplotlib【グラフ描画ライブラリ】使用

import random
import matplotlib.pyplot as plt

# 初期設定
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.sans-serif'] =\
    ['Yu Gothic', 'Hiragino Maru Gothic Pro', 'Noto Sans CJK JP']
fig, axs = plt.subplots(
    3, 4,
    figsize=(12, 9),
    tight_layout=True,
)
plt.suptitle('実数値分布')

# betavariate()【ベータ分布】
alpha = 2
beta = 5
data = [random.betavariate(alpha, beta) for i in range(10000)]
axs[0, 0].hist(data, bins=100)
axs[0, 0].set_title(f'betavariate({alpha}, {beta})\n【ベータ分布】')

# expovariate()【指数分布】
lambd = 1.0
data = [random.expovariate(lambd) for i in range(10000)]
axs[0, 1].hist(data, bins=100)
axs[0, 1].set_title(f'expovariate({lambd})\n【指数分布】')

# gammavariate()【ガンマ分布】
alpha = 7.5
beta = 1.0
data = [random.gammavariate(alpha, beta) for i in range(10000)]
axs[0, 2].hist(data, bins=100)
axs[0, 2].set_title(f'gammavariate({alpha}, {beta})\n【ガンマ分布】')

# gauss()【ガウス分布】
mu = 0
sigma = 1.0
data = [random.gauss(mu, sigma) for i in range(10000)]
axs[0, 3].hist(data, bins=100)
axs[0, 3].set_title(f'gauss({mu}, {sigma})\n【ガウス分布】')

# lognormvariate()【対数正規分布】
mu = 0
sigma = 0.25
data = [random.lognormvariate(mu, sigma) for i in range(10000)]
axs[1, 0].hist(data, bins=100)
axs[1, 0].set_title(f'lognormvariate({mu}, {sigma})\n【対数正規分布】')

# normalvariate()【正規分布】
mu = 0
sigma = 1.0
data = [random.normalvariate(mu, sigma) for i in range(10000)]
axs[1, 1].hist(data, bins=100)
axs[1, 1].set_title(f'normalvariate({mu}, {sigma})\n【正規分布】')

# paretovariate()【パレート分布】
alpha = 20
data = [random.paretovariate(alpha) for i in range(10000)]
axs[1, 2].hist(data, bins=100)
axs[1, 2].set_title(f'paretovariate({alpha})\n【パレート分布】')

# random()【一様分布】
data = [random.random() for i in range(10000)]
axs[1, 3].hist(data, bins=100)
axs[1, 3].set_title('random()\n【一様分布】')

# triangular()【三角分布】
low = 0.0
high = 1.0
mode = 0.5
data = [random.triangular(low, high, mode) for i in range(10000)]
axs[2, 0].hist(data, bins=100)
axs[2, 0].set_title(f'triangular({low}, {high}, {mode})\n【三角分布】')

# uniform()【一様分布 (範囲指定)】
a = 50
b = 100
data = [random.uniform(a, b) for i in range(10000)]
axs[2, 1].hist(data, bins=100)
axs[2, 1].set_title(f'uniform({a}, {b})\n【一様分布 (範囲指定)】')

# vonmisesvariate()【フォン・ミーゼス分布】
mu = math.pi
kappa = 4
data = [random.vonmisesvariate(mu, kappa) for i in range(10000)]
axs[2, 2].hist(data, bins=100)
axs[2, 2].set_title(f'vonmisesvariate({mu:1.3}, {kappa})\n【フォン・ミーゼス分布】')

# weibullvariate()【ワイブル分布】
alpha = 5
beta = 2
data = [random.weibullvariate(alpha, beta) for i in range(10000)]
axs[2, 3].hist(data, bins=100)
axs[2, 3].set_title(f'weibullvariate({alpha}, {beta})\n【ワイブル分布】')

# 表示
plt.show()
randomの実数値分布関数